Abusing the Harvard Architecture in Nand2Tetris Assembly

Every now and then, when one writes assembly code by hand, one notices opportunities for optimisation.

Some are concise and elegant, it’s usually a good idea to use those.

Some are complicated or convoluted, you might use them if the benefit they bring is significant.

Then there are those who are outright ludicrous. You’d never use these in any production code, but if you think of one, you’re definitely going to jokingly suggest it to your coworkers just to see their horrified faces. Or maybe write about them in a blog post.

Nand2Tetris? #

I attempted to write this post assuming no prior knowledge of Nand2Tetris. In case you are familiar with the course and its assembly language, feel free to skip to the Challenges.

Nand2Tetris is a wonderful course where one learns the basics of hardware and software from the ground up by designing a CPU and writing a compiler stack for it, culminating in the development of an application, e.g., Tetris.

Normally, one goes through this course once (in my case, as part of a degree), learns a bunch and never touches any of the material again, since the CPU, the assembly language and the compiler stack are all invented by the course and don’t occur in the wild.

Nevertheless, more than 10 years after I finished the course, I still find myself playing with the Nand2Tetris assembly, and apparently, others do as well.

A shot from the TV show Arrested Development turned into a meme. A man stands with his back to the camera. Overlaid text says: "There are dozens of us, dozens!"

Why Nand2Tetris Assembly? #

You’re probably wondering why working with Nand2Tetris assembly can be more interesting than working with something that does exist in the real world, such as x86 or ARM.

It is precisely the disconnect from reality that makes it appealing.

First, as an educational tool, the CPU is very simple in design. Depending on how you count, it has ~19 documented opcodes (and 14 undocumented ones). Compared to real-world alternatives, this is a very low knowledge barrier - you don’t have to remember countless instructions or constantly consult an online reference.

Second, unlike real-world architectures, there is only one implementation of the CPU. Sure, different people write slightly different designs, but they all execute exactly one instruction per clock cycle. That makes instruction count a great metric for how optimised an algorithm is. Compare this with x86 and its many processors, each having vastly different performance characteristics for the same instruction.

Nand2Tetris CPU Architecture #

I’m not going to go into the fine details of the architecture, but luckily, as I mentioned before, there aren’t that many details to begin with.

It is most likely that you’re reading this on a device using the von Neumann architecture, where the data and the program all reside in the RAM, hopefully in different addresses.

Our CPU, on the other hand, uses the Harvard architecture. In this architecture, there are separate memories for the data and for the program, in our case, they are named RAM and ROM, respectively.

The CPU has two 16-bit registers:

D - Multi-purpose register. Doesn’t have any special uses.
A - Load/Pointer register:
1. Can load any 15-bit integer value.
2. Can be used as a pointer for reading/writing values from/to the RAM.
3. Can be used as a pointer to an instruction in the ROM to which the program can jump, thereby implementing flow control.

In addition, there’s a fake register, M, representing the contents of the memory address pointed to by A (you can think of it as *A).

The instructions come in two types as well:

Load Instruction - Sets A to a 15-bit integer. Its assembly representation is @<integer>, e.g., @7447 or @32223.
Compute Instruction - performs a computation on 0 to 2 of the registers, optionally stores the result into any combination of registers and optionally jumps to the instruction in the ROM pointed to by A. Its assembly representation is
[<destination_registers>=]<computation>[;<jump_condition>],
e.g., AD=A+D (set A and D to their sum), D;JEQ (jump if D equals 0), D=D+1;JMP (increment D by 1 and then jump unconditionally).

And that’s it!

The Challenges #

As you might have noticed, the A register has too many hats. Whenever we want to access the memory, A needs to hold the relevant RAM address. Whenever we want to implement any type of flow control, A needs to hold the relevant ROM address.

In practice, that means A can’t store any values long-term, since A needs to change all the time. Let’s look at the following example implementing an absolute value operation:

    // The program calculates the absolute value of RAM[0]
    // in place

0   @0                  // Load 0 into A
1   D=M                 // Load the value in the RAM in the address A into D
2   @ALREADY_POSITIVE   // Load the ROM address of (ALREADY_POSITIVE) into A
3   D;JGE               // if D >= 0 then jump to the address in A
4   @0                  // Load 0 into A
5   M=-M                // Negate M
    (ALREADY_POSITIVE)  // Not an instruction, just a label referring to the
                        // index of the next instruction in the ROM - 6
6   <Whatever is after> // Rest of the ROM

Even in such a short code excerpt, we had to set the values of A 3 times.

The reality is actually grimmer. Pay attention to how the jump condition checks whether D is greater than 0. Recall that when jumping, A is reserved for the jump target, therefore it cannot be used for the condition. M can’t be used either, as it depends on A, and since A is reserved, M is the contents of whatever arbitrary RAM address A points to, which is most likely not the one you’d actually like to check.

This means that D is actually special as well, as it needs to be used for jump conditions.

The consequence is that when implementing any non-trivial algorithm, you find yourself solving a river crossing puzzle, spending most of the instructions putting values into and out of the RAM, as the registers are always needed for something else.

Optimisation is then focused on removing this unnecessary overhead.

Abusing the Harvard Architecture I #

In our absolute value implementation above, in the worst case, we won’t jump and run all 6 instructions, and in the best case, we do jump and only run 4 instructions.

The main culprit for the code being so long is that we had to copy the value into D since A could either serve as a RAM address (so we can use M) or a ROM address (so we can jump).

But what if A could serve as both at the same time?

Earlier, we said that when A is reserved for the jump, M is the contents of whatever arbitrary RAM address A points to. The key observation is that arbitrary doesn’t mean random. What if we could decide where our input and output are?

Let’s assume our code starts at address 0 in the ROM, and unlike last time, our input is at RAM[3].

We can then shrink the absolute value implementation to the following:

    // The program calculates the absolute value of RAM[3]
    // in place

0   @3                  // Loads 3 into A, equivalent to
                        // @ALREADY_POSITIVE
1   M;JGE               // if M >= 0 then jump to the address in A
2   M=-M                // Negate M
    (ALREADY_POSITIVE)  // Not an instruction, just a label referring to the
                        // index of the next instruction in the ROM, in this
                        // case 3
3   <Whatever is after> // Rest of the ROM

If the input is positive, we’ll jump over the last instruction (M=-M) and execute only 2 instructions, while if it’s negative, we’ll also run the last instruction, resulting in a worst-case of 3 instructions.

That’s half as many as in the naive version!

Thanks to the Harvard architecture, the pointer with the value 3 has two meanings at the same time:

The RAM address of the input/output
The ROM address of the end of our code

This saves us the unnecessary shuffling of A, which, going back to the river-crossing metaphor, means our boat is actually bigger than we thought!

Sure, this example is a bit contrived since we needed the input in the arbitrary address 3, but in a way, that’s exactly the point. We see how having the relevant data in specific RAM addresses can help us implement the same algorithm more efficiently.

Now let’s see this principle in action with a less contrived, but more complex example.

Optimising Fib(n) #

Our next algorithm is calculating the nth Fibonacci number mod 2¹⁶ (since our word/register size is 16-bit). We do this by generating the whole series until reaching the nth element. Here’s the algorithm in C-like pseudocode:

previous = 1;
result = 0;
while (n > 0) {
    temp = previous;
    previous = result;
    result = result + temp;
    n = n - 1;
}

Note: we initialise previous to 1 as this would be the -1^th element of the series if it were generalised to negative indices.

A straightforward Nand2Tetris assembly implementation would be something like this (annotated with the respective pseudocode lines):

// The program calculates the RAM[0]th Fibonacci number
// and writes the result into RAM[1].

// previous = 1;
@PREVIOUS
M=1

// result = 0;
@1
M=0

// while (n > 0) {
@0
D=M
@END
D;JLE

(LOOP)

    // temp = previous;
    @PREVIOUS
    D=M
    @TEMP
    M=D

    // previous = result;
    @1
    D=M
    @PREVIOUS
    M=D

    // result = temp + result;
    @TEMP
    D=M
    @1
    M=D+M

    // n = n - 1;
    @0
    MD=M-1

    // }
    @LOOP
    D;JGT
(END)

How do we measure its performance? We run the code on all valid inputs and count the number of executed instructions in the worst case.

When optimising, we will focus on the body of the loop - the lines between (LOOP) and (END) - since every instruction in the loop is executed many times, while the instructions outside the loop are only executed once.

Results #

For this implementation, we have:

Length of loop body: 16 instructions
Worst case: 524280 executed instructions

Tweaking the Algorithm #

The first thing we could do to reduce the number of instructions in the loop is to reduce the work our algorithm does in every iteration.

Instead of:

temp = previous;
previous = result;
result = result + temp;

We do:

result = result + previous;
previous = result - previous;

which has the identical result - advancing result and previous by one element.

This shrinks our loop code to:

(LOOP)
    // result = result + previous;
    @PREVIOUS
    D=M
    @1
    MD=M+D

    // previous = result - previous;
    @PREVIOUS
    M=D-M

    // n = n - 1;
    @0
    MD=M-1

    // }
    @LOOP
    D;JGT
(END)

Results #

We get an improvement of ~37%:

Length of loop body: 10 instructions
Worst case: 327678 executed instructions

The next step is to start playing with the memory layout.

Abusing the Harvard Architecture II #

Let’s look at the end of the loop:

    // n = n - 1;
    @0
    MD=M-1

    // }
    @LOOP
    D;JGT
(END)

We decrement n, which is placed in the address 0 in the RAM, and then if the result is greater than 0, we jump to (LOOP) (the beginning of the loop).

These two parts must be done separately, since A needs to be set to 0 when we decrement n, and it needs to be set to the address of (LOOP) in the ROM when we make the jump. This limitation would disappear if somehow the RAM address of n and the ROM address of (LOOP) were the same.

We can’t move (LOOP) to address 0, since that’s the start of the program, so let’s move n to the RAM address equal to the ROM address of LOOP, which we will refer to as *LOOP. We can do this by simply copying n into that address before the loop starts:

previous = 1;
result = 0;
*LOOP = n;
while (*LOOP > 0) {
    result = result + previous;
    previous = result - previous;
    *LOOP = *LOOP - 1;
}

for which the assembly would be:

// previous = 1;
@PREVIOUS
M=1

// result = 0;
@1
M=0

// *LOOP = n;
@0
D=M
@LOOP
M=D;

// while (*LOOP > 0) {
@END
D;JLE

(LOOP)
    // result = result + previous;
    @PREVIOUS
    D=M
    @1
    MD=M+D

    // previous = result - previous;
    @PREVIOUS
    M=D-M

    // *LOOP = *LOOP - 1;
    // }
    @LOOP
    M=M-1;JGT
(END)

Results #

Once again, shrinking the loop body nets us better performance:

Length of loop body: 8 instructions
Worst case: 262146 executed instructions

The 2 instructions we added before the loop are inconsequential compared to removing 2 instructions from every iteration of the loop.

While a 20% improvement is not insignificant in itself, in addition to the immediate benefit, a new opportunity for optimisation just opened up.

Register Allocation #

Our latest step converted this:

    // n = n - 1;
    @0
    MD=M-1

    // }
    @LOOP
    D;JGT
(END)

into that:

    // *LOOP = *LOOP - 1;
    // }
    @LOOP
    M=M-1;JGT
(END)

The new code is not only shorter, it also has another quality to it - unlike the old code, it doesn’t read D or change it.

Thanks to that, D can now keep its value between iterations, allowing us to allocate it to a variable. Specifically, we’re going to use it to store previous instead of having it in the RAM.

Before:

(LOOP)
    // result = result + previous;
    @PREVIOUS
    D=M
    @1
    MD=M+D

    // previous = result - previous;
    @PREVIOUS
    M=D-M

After:

(LOOP)
    // result = result + previous;
    @1
    M=M+D

    // previous = result - previous;
    D=M-D

And the full code:

// The program calculates the RAM[0]th Fibonacci number
// and writes the result into RAM[1].

// result = 0;
@1
M=0

// *LOOP = n;
@0
D=M
@LOOP
M=D;

// while (*LOOP > 0) {
@END
D;JLE

// previous = 1; ** Note: This is still outside the loop body **
D=1

(LOOP)
    // result = result + previous;
    @1
    M=M+D

    // previous = result - previous;
    D=M-D

    // *LOOP = *LOOP - 1;
    // }
    @LOOP
    M=M-1;JGT
(END)

Results #

Here we get:

Length of loop body: 5 instructions
Worst case: 163844 executed instructions

That’s a whopping 50% less than the second implementation - our last version without the hack.

This last step reveals the real benefit of this trick. Without it, we had no registers that could be allocated to variables long-term.

We needed to use both A and D whenever we had a conditional branch, for the target and the condition, respectively.

With the trick, D is no longer required for the condition, so the number of available registers skyrockets from 0 to 1. This allows us more flexibility, and the code becomes simpler and faster.

Summary #

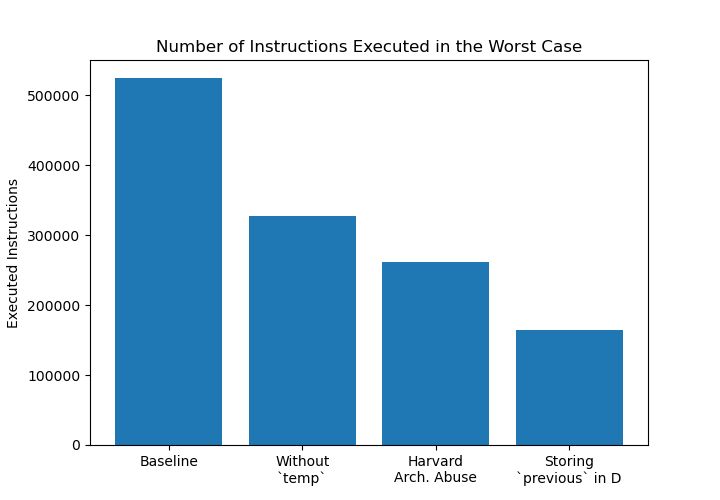
Bar chart comparing the results previously mentioned in this post. It shows the number of instructions executed in the worst case for the different versions: Baseline - 524280, Without `temp` - 327678, Harvard Arch. Abuse - 262146 and Storing `previous` in D - 163844.

In total, we reduced the runtime of the worst case by almost 69 percent from the baseline to our final version.

Neither dropping temp in favour of smarter arithmetic, nor allocating a register (D) to store previous, is Nand2Tetris-specific. Compilers do similar things all the time on many real-world platforms.

Storing n in *LOOP, however, could only be done on a Harvard architecture machine with separate data and instruction memory.

So at first glance, it might look like only one out of our three optimisations, the one bringing the smallest improvement, relied on the Harvard architecture. This is, however, misleading, since the last optimisation (storing previous in D) depended on the previous two, and it, as well, was only made possible by the Harvard architecture.

Application #

Since we usually have full control of the program running on the Nand2Tetris computer, this trick is entirely viable. Very hot code paths, such as multiplication and division functions, can be made significantly faster with this approach, thereby speeding up an entire program.

Another advantage is reducing the code’s size, allowing us to cram more into our modest ROM of only 32768 instructions.

The difficulty in this method is ensuring we don’t mess up data that other parts of our program store in the addresses that happen to coincide with the addresses we want to use, but this is solvable.

We can invest a few instructions in saving the existing values before the function runs and restoring them afterwards, or even better, we can prevent collisions entirely by putting these functions in the ROM, where the respective RAM addresses are those reserved for static variables.

Further Optimisations of Fib(n) #

Our last version is far from optimal. Even with the same algorithm, it is possible to improve performance by up to a further ~80% with other techniques, such as loop unrolling, that might feature in a future blog post.

Changing the algorithm to one with a lower complexity might give even better results, but that would require a fast multiplication implementation, an interesting challenge in itself.

If you have any further ideas or interesting techniques, I’d love to hear them! Feel free to contact me by Email or through Mastodon.